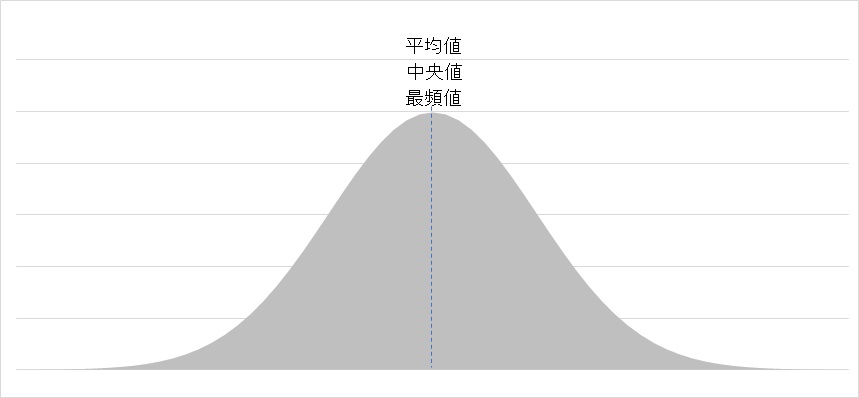
正規分布は、中央が一番頻度が大きく、左右対称で滑らかで美しい形の分布だ。「平均値」と「中央値」と「最頻値」が同一でかつ中心となり、その中心から離れるにしたがいカーブしながら下線に近づいていく、富士山のようなきれいな形をしている。
自然現象でも社会現象でも、世の中の多くの現象は正規分布に近い分布となる。たとえば、ヒトの身長、そのほか動物の体長、植物のサイズ、製品の重さやサイズ、などを測定してグラフをつくれば、正規分布に近い分布となるだろう。
このことを、正規分布に近似するといい、正規分布に近似しているのであれば、実用上、正規分布として取り扱うことができる。
食品のデータも正規分布する
なにか食品の製品をつくるときのことを考えてみよう。たとえば内容量100g入の缶詰を作るとしよう。製品は設計段階で規格値が定められる。この缶詰は100gの内容量にしようと決めて設計を描き、それができるように製造機械の設定・調整をし、製造をしていく。
でも、いくら機械の設定を100gの充填になるようしたといっても、すべての缶詰が100gピッタリとなるわけではなく、0.1g単位でみれば、99.5gの缶詰もあれば、100.5gの缶詰もできてしまうはず。0.1g単位の測定機器で100.0gと表示された缶詰も、もっと精密に測定できる機器をつかえば、100.03gのような重量になっているかもしれない。
このように出来上がる製品の重量は、設計でねらった数値から多かれ少なかれ誤差が生まれるものだ。製品としては規格範囲があり、その範囲内であれば問題なく製品化される。
誤差が生じてしまうとはいっても、目標としてねらっている重量があるので、出来上がった製品群を測定すれば、そのねらいの重量付近の製品が一番多くなっている。ねらった重量から少しだけ誤差のある製品も多めにつくられてしまう。しかし、ねらった重量よりもかなり重いもの、逆にかなり軽いものは、よっぽどの失敗をしないとつくられないので、発生は少なくなる。缶詰の例では、100g付近の缶詰が多く、100gから10gも20gも離れた重量の缶詰は、ほぼ発生しない。
このように、ねらった目標の規格値どおりの製品をつくろうとすると、その値が出来上がった製品群の平均値となり、目標値付近の製品がたくさんでき、目標値から離れるたものほど製品数は少なくできるものなのだ。
測定した値をグラフにすれば、上に記載した正規分布のような形になる。ものづくりの製品の重量やサイズの数値なども正規分布に近似するのだ。
誤差を表した分布であるともいえるので、正規分布は誤差曲線とも呼ばれる。
正規分布は平均値と標準偏差で決まるのが特徴
正規分布は平均値と標準偏差で決まる
正規分布は、平均値と標準偏差の2つの値でどのような分布になるのかが決まる。平均値は分布グラフの中央の値となり、標準偏差は山の広がり具合を決める。
ところで、平均値を記号で表すとμ、標準偏差を記号で表すとσとなる。これらをつかって正規分布を略記すると、
N(μ,σ2)
と表記される。NはNormal distribution(正規分布)の頭文字、μは平均値、σ2は分散で、正規分布は平均値と標準偏差で決まることが、これら2つの値だけで表記されることからもわかるだろう。標準偏差は分布の山の広がり具合を決めるので、値が小さければ急峻な岩峰のような形になり、バラつきが小さい分布となる。標準偏差の値が大きければ裾が広がったのっぺりとした丘のような形になり、バラつきは大きい分布になる。
平均値は同じままで標準偏差を変えてみる
平均値や標準偏差を変えると、どのように分布が変わるのかをグラフで見てみよう。
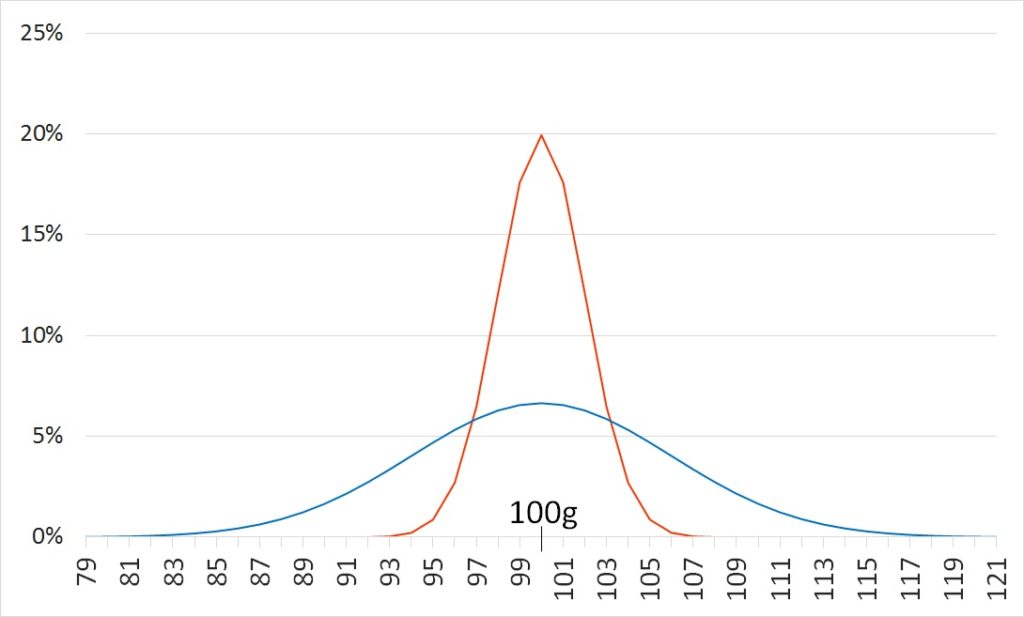
平均値は同じままで、標準偏差だけを大きくすると、分布のてっぺんの位置は同じままで、山がのっぺりと広がるようになる。
赤色: N(100,22)
青色: N(100,62)
標準偏差は同じままで平均値を変えてみる
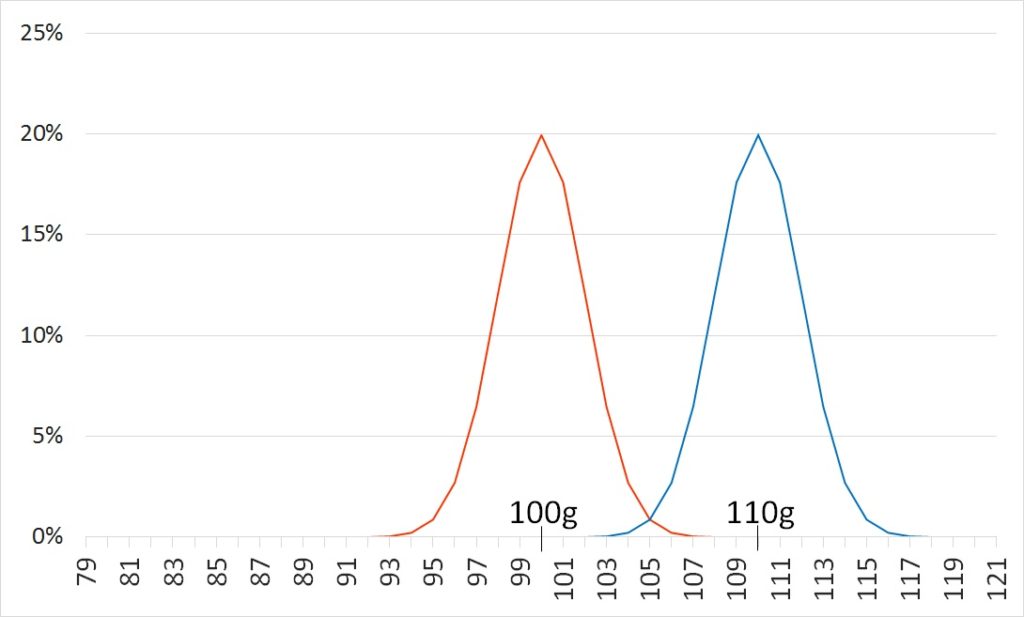
標準偏差は同じままで、平均値だけ変化させてみよう。山の形はそのままで、平均値が小さくなると左へ、平均値が大きくなると右へ動く。
青色: N(100,52)
赤色: N(110,52)
コメント