データの値の範囲をいくつかに区切り、その区切った中に含まれるデータの数をまとめた表が度数分布表で、その度数分布表を柱状図として表わしたものが、ヒストグラムだ。
ヒストグラムの作り方
食品の製品重量を計測し、120個の重量データが得られたとしよう。
109、109、111、105、102、 107、107、110、114、112、109、105、118、108、109、110、 105、115、113、113、111、122、111、116、109、110、111、107、 97、104、110、111、110、118、116、104、116、107、118、112、 112、112、112、117、111、114、112、108、 102、112、116、113、108、115、118、116、114、116、104、119、117、105、112、107、109、118、119、112、107、109、115、111、111、121、114、・・・・・・・・・・
※単位: g
・・・集まったデータは単なる数字の羅列である。これだけデータの数が多くなってくると、そのまま見ているだけでは、なにがどうなっているのか、さっぱりわからない。
これらのデータがどのような分布をしているのか確認するために、ヒストグラムを作成してみることにしよう。
まずデータを度数分布表にまとめる。食品の重量などであれば、ヒストグラムの区間の(柱)は10個前後がよい。データを分類するための区画をそれぞれ「階級」といい、~102の階級、~105の階級それぞれのデータがあてはまる階級にカウントしていく。
☆ヒストグラムの用語の説明
ヒストグラムは、横軸に測定値、縦軸に区間の度数の柱を立てた柱状図だ。
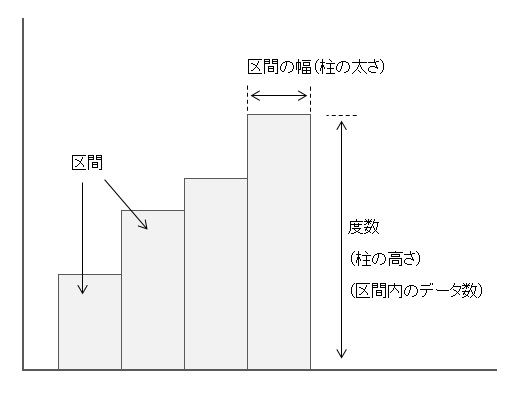
区間の数を10にしたいのであれば、
データの範囲 ÷ 区間の数 10 = 区間の幅
で、区間の幅を何gにしたらよいか計算できる。上記のデータは、最大値が124、最小値が96で、その範囲は28だ。区間の数を10にするには、
データの範囲 28 ÷ 区間の数 10 = 2.8
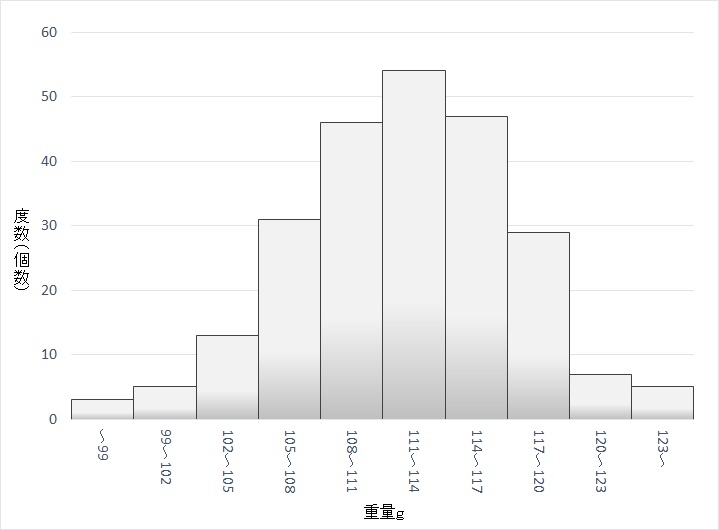
となるので、四捨五入して区画の幅を3として、度数分布表を作成した。「99~102」とは「99以上~102未満」のことだ。
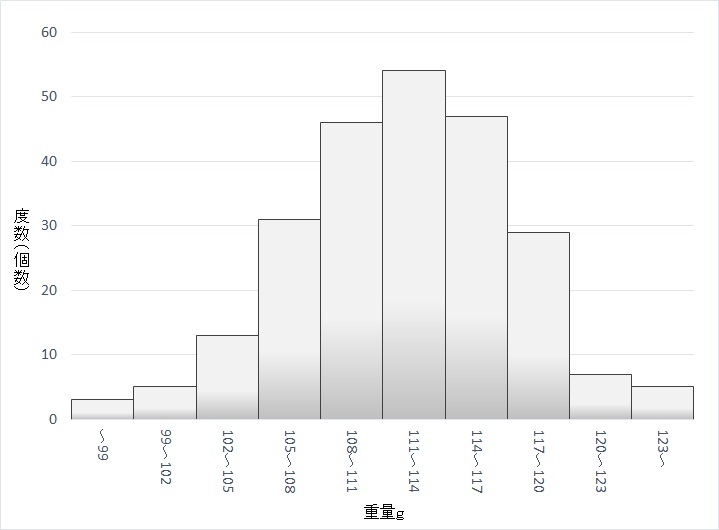
| 区間の境界値 | 度数 |
| ~99 | 3 |
| 99~102 | 5 |
| 102~105 | 13 |
| 105~108 | 31 |
| 108~111 | 46 |
| 111~114 | 54 |
| 114~117 | 47 |
| 117~120 | 29 |
| 120~123 | 7 |
| 123~ | 5 |
単位:g
この度数分布表をそのままグラフにすればよい。
ヒストグラムの区間(柱)の数
ヒストグラム区間(柱)の数、つまり階級は10前後がいいと書いた。その理由は、階級の数が少なくすればするほど、 ヒストグラム自体はすっきりするのだが、ヒストグラムから読み取れる情報が減ってしまうからだ。
逆に、階級の数を多すればするほど、並んだ柱が歯抜け状態になってしまい、ヒストグラム全体の形がわかりづらくなってしまうのだ。
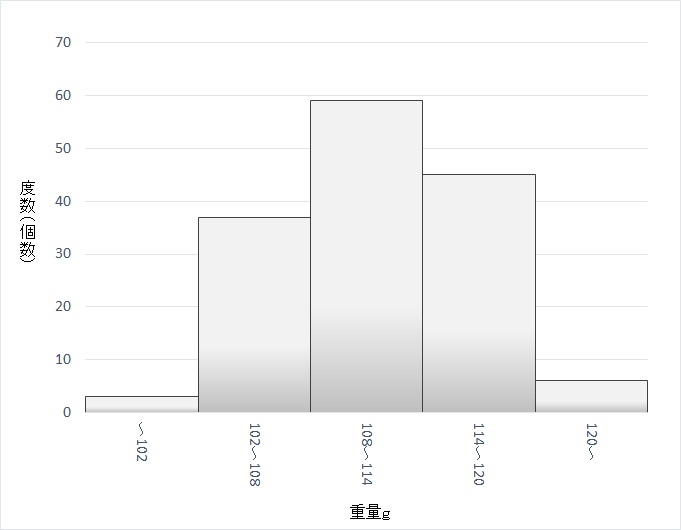
☆階級の数を5つにしてみる
図太い形のヒストグラムになってしまい、データの詳細がまったくわからない。
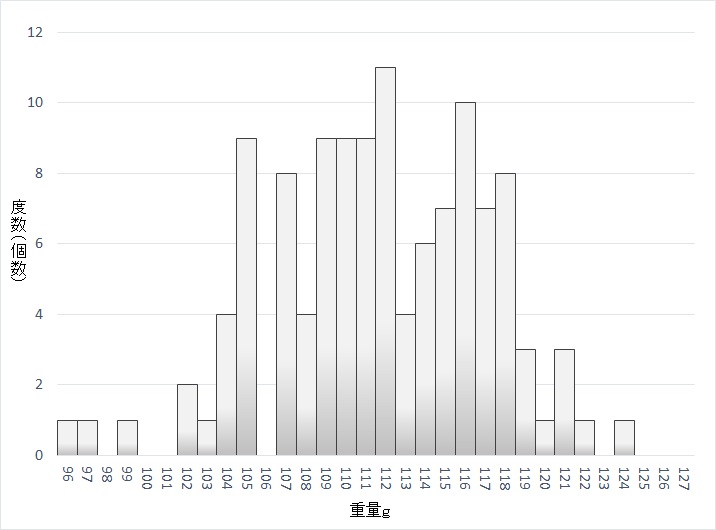
☆区画の幅を1gにして階級数を28にしてみる
歯抜け型になってしまい、分布の形が読み取りづらくなってしまいました。
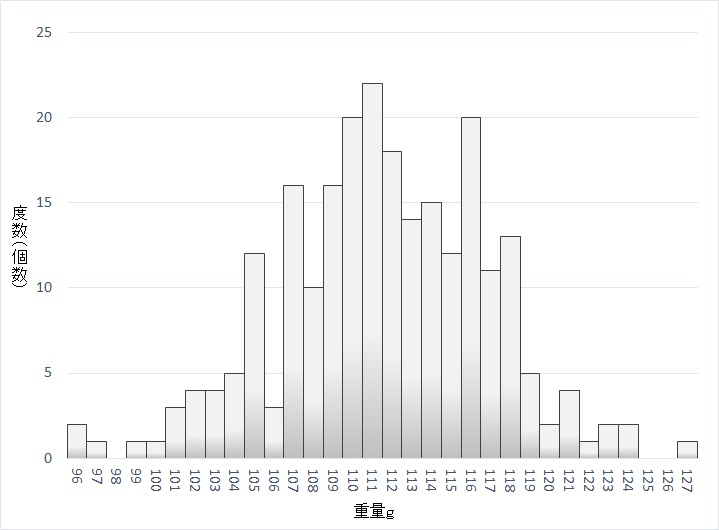
ただし、階級が多くあっても、データ数をもっと増やしていくと、歯抜けもなくなり、しっかりとした山型の分布が得られるようになる。240個の製品を計測すると、下図のようになる。多少ガタガタはしていますが、歯抜けが減少して山の形が見えてきました。
☆240個計測してみた
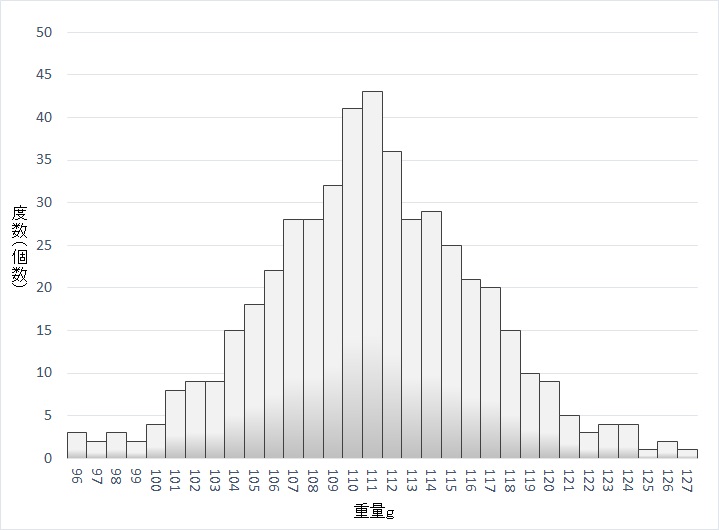
480個の製品を計測してヒストグラムにまとめると、無事に歯抜けの無いきれいな山型になった。区画の幅を小さくしすぎると、こうなる。
※480個計測してみた
コメント