散布図の用途と作り方、散布図で確認することができる相関関係について解説した。
散布図とは
縦軸と横軸に目盛りを設けたグラフに2つの変数のデータをプロット(打点)した図で、2つの変数間の関係を見るためのものだ。一方が増えるともう一方はどう変化するのか、一方が減るともう一方はどう変化するのか、2つの変数の関係を散布図から読みとることができるのだ。
たとえば、
- ヒトの身長と体重の関係
- ヒトの親と子の身長の関係
- 国語テストの得点と英語テストの得点
などだ。ヒトは身長が高ければ体重も重くなり、遺伝的に背の高い親からは背の高い子供が生まれる傾向があるだろう。
ここに、とあるテストの結果がある。国語と英語のテストだ。この2つの科目のテストの得点に、どのような関係があるのか散布図で見てみよう。
散布図をつくって見てみる
ここに10人の国語のテスト、英語のテストの結果がある。この2つの科目のテストの得点に、 どのような関係があるのか散布図で見てみよう。
10人の国語の得点、英語の得点
| 国語の得点 | 英語の得点 | |
| 後藤 | 50 | 40 |
| 小籔 | 80 | 70 |
| 児島 | 10 | 5 |
| 吉田 | 60 | 50 |
| 角田 | 60 | 60 |
| 豊本 | 60 | 90 |
| 飯塚 | 90 | 85 |
| 小林 | 65 | 35 |
| 遠藤 | 70 | 55 |
| 沼田 | 40 | 35 |
後藤の得点をプロットする。国語は50点、英語は40点だ。横軸を国語の得点、縦軸を英語の得点として、その2つが交わる箇所に点を打つ。
次に小籔の国語得点80点と英語の得点70点もプロットする。
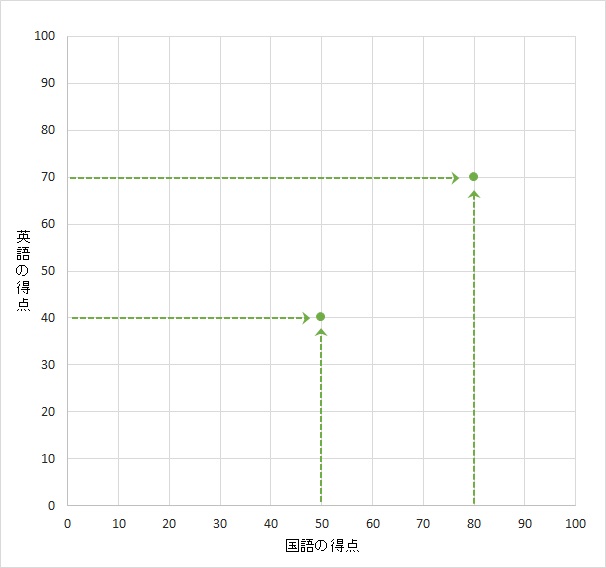
このようにして10人分の得点をプロットしていくと、下のような散布図が完成する。
☆散布図 完成
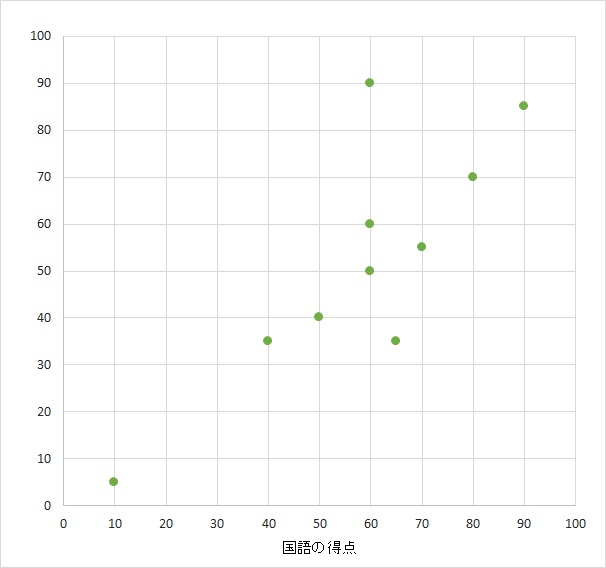
散布図を見るとどうだろうか。なんとなく右肩上がりになっているように見える。打点に沿って線を引くとそれがよくわかる。
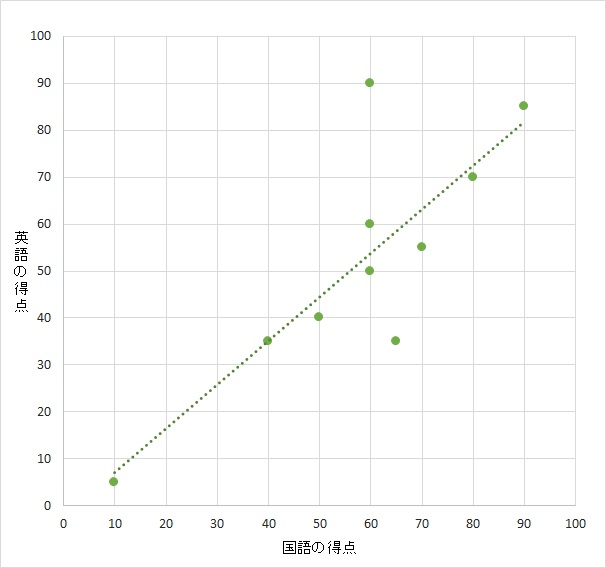
これは、横軸である国語の得点が高ければ高いほど、縦軸の英語の得点も高くなっていることを示している。
このように、2つの変数のうち一方の値が大きければ、もう一方の値も大きくなる傾向があることを、「正の相関がある」という。このグラフであれば、「国語の得点と英語の得点の間に正の相関がある」わけだ。
逆に一方の値が大きくなると、もう一方の値が小さくなる傾向があれば、「負の相関がある」という。
相関関係の言い表し方
一方をxとし、もう一方をyとすると、相関関係について下記のように言い表す。番号をふった図も合わせて見てほしい。
(1)xが大きくなったときに、yも同様に大きくなる
⇒「xとyの間に強い正の相関がある」
(2)xが大きくなったときに、yも大きくなる傾向がある
「xとyの間に正の相関がある」
(3)xが大きくなったときに、yも大きくなるわけでなく、散布図上にバラバラに打点されている
⇒「相関が無い」
(4)xが大きくなったときに、yも小さくなる傾向がある
⇒「xとyの間に負の相関がある」
(5)xが大きくなったときに、yも同様に小さくなる
⇒「xとyの間に強い負の相関がある」
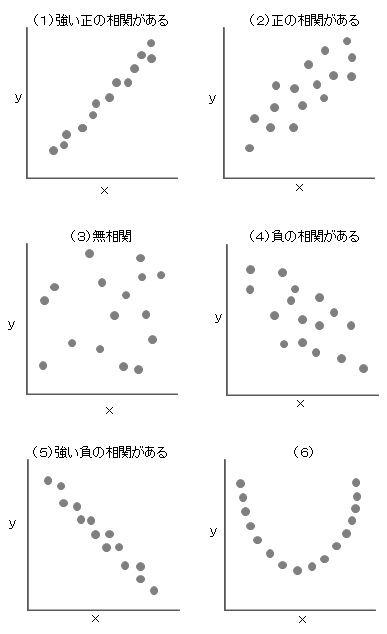
これらの相関関係がどれだけあるのかを示すものとして、相関係数という数値がある。相関係数は、-1 ~ 0 ~ +1の間の値をとり、正の相関があるとプラスの側に大きくなり、負の相関があるとマイナス側に小さい数値となる。
正の相関が強いほど相関係数は+1に近づき、(1)のような図になるのだ。(1)の図は相関係数0.9程だ。
相関係数=1の場合には、2つの変数が完全に連動していて、打点を完全に直線で結ぶことができる。正の相関が弱くなるほど相関係数は0に近づいていき、0だと全く相関が無い状態だ(無相関)。
(4)のような負の相関では、相関係数はマイナスの値をとる。
ちなみに、先ほど散布図を書いた10人のテスト結果で、国語の得点と英語の得点の相関係数は、0.81となっているので、英語の得点と国語の得点には、なかなか強い相関関係があるとわかる。

ただし、ここでは10人だけのデータで相関係数を出したわけだが、実は10個のデータでは精度が高くない。実際に活用する場合にはもっと多くのデータ(30個以上)を集めた方がよい。
補足情報だが、グラフ上での打点の集まりの傾きは、傾きがないほうが相関が弱い気がしてしまうが、じつは相関の強さ・弱さにいっさい関係がない。バラつきが大きいか、バラつきが小さ直線的になっているかどうかが、相関の強弱となる。
ためしに、
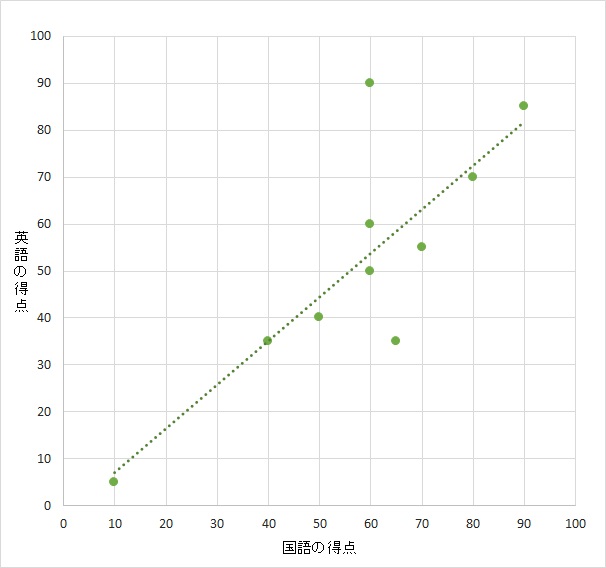
- もともとのグラフ
- 縦軸の目盛りを故意に200までにしたグラフ
- 全体の形を正方形から長方形に変えたグラフ
を下に用意した。打点上に引いた線の傾きは簡単に変わる。だが、当然のごとく各人の得点と相関係数は当然変わらず、相関の強さも変わらない。

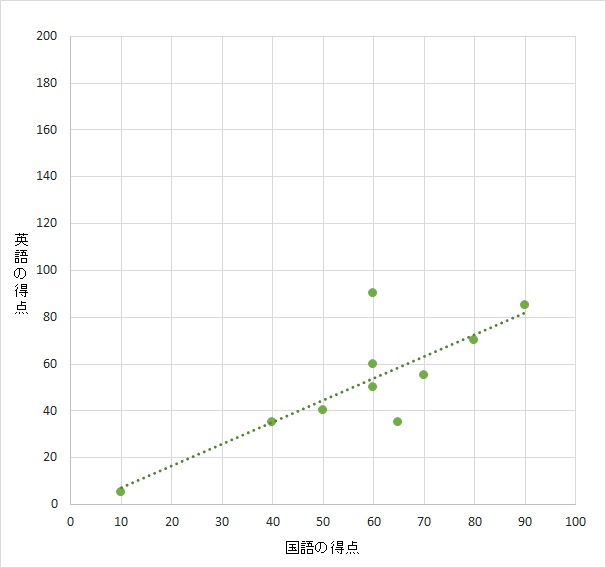
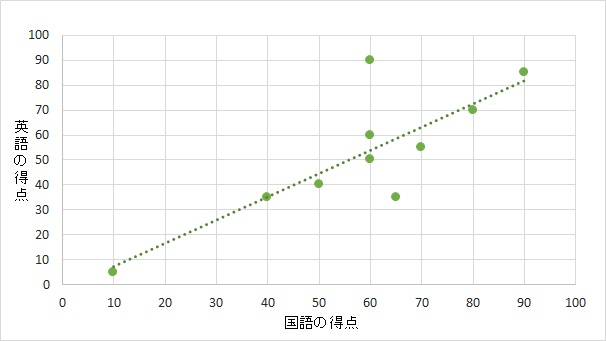
傾きは変わったとしても、傾きと相関係数は関係がないことがわかる。
コメント